Polygon – Shape, Types, Formulas, Examples

If you look around yourself, you can see objects of different forms, colour and appearance. The outline of the external form of something is defined as its shape. The objects around us exhibit a plethora of shapes. Basic idea about the shapes of objects is provided to the kids in geometry, a branch of mathematics. Today, let’s learn about the polygons. So, first question that clicks in the mind is: what is a polygon? To answer this question in simplest way we can say that a polygon is a 2-dimensional closed figure formed by three or more straight line segments. The line segments that form the polygon are called its sides or edges, and the points where the sides meet are called vertices. A polygon should have at least three straight sides and angles, but typically the shapes having five or more sides and angles are called as polygons. The sides of polygon cannot be less than three in number because it needs a minimum of 3 sides to be a closed shape or else it will be open.

A polygon has some properties which are:

A polygon is made up of straight lines only.

A polygon is a closed shape i.e. all sides are connected to one another at both ends.

A polygon has vertices which are the corners or points where two sides meet.

A polygon is a 2D structure i.e. lies in a plane.

Polygons  are classified into various types based on several factors which include (i) number of sides, (ii) length of sides, (iii) highest angle and (iv) intersection of the edges.

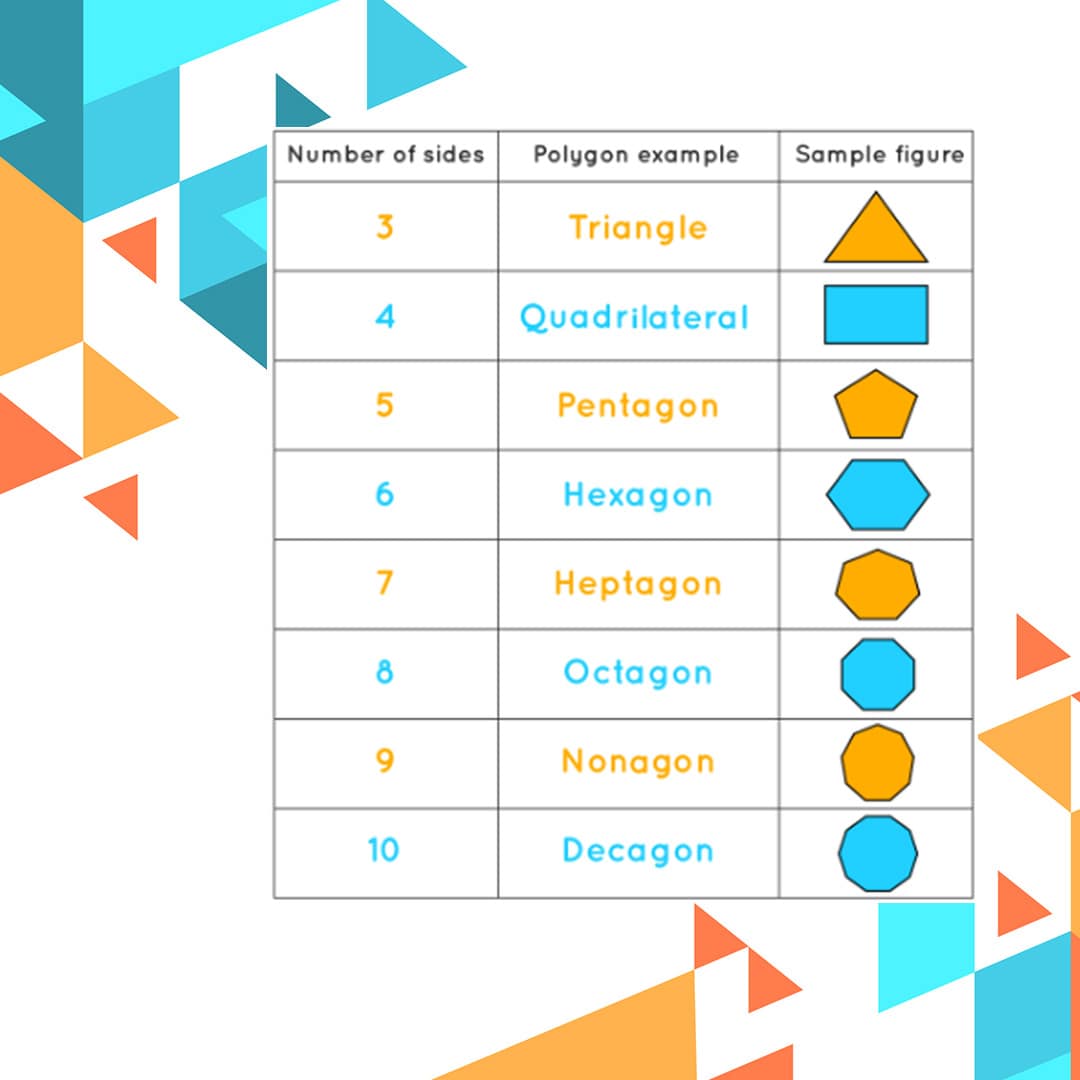
Based on the number of sides polygons can be triangles (3 sides), quadrilateral (4 sides), pentagon (5 sides), hexagon (6 sides), heptagon (7 sides), octagon (8 sides), nonagon (9 sides), decagon (10 sides), and so on. Theoretically, the maximum number of sides a polygon can have is infinite as long as the sides form a closed shape without intersecting. 

Based on side Lengths and angles a polygon can be either a regular polygon with all sides and angles equal  or an irregular polygon with different lengths of sides and angles at vertices. Examples of regular polygon are  square, equilateral triangle. Examples of irregular polygon are  scalene triangle, rectangle etc.

Based on the degrees of angles a polygon can be wither convex polygon or a concave polygon. In a convex polygon all angles are less than 180° (e.g., square, triangle). In a concave polygon, on the other hand, at least one angle is more than 180° (e.g., arrowhead shape).

Based on the intersection of the edges polygons can be either simple or complex. In a simple polygon there is only one boundary. The sides of a simple polygon do not intersect. On the other hand, a complex polygon is a polygon whose sides cross over each other one or more times. Like when you a star by combining two triangles, it is a complex polygon.

Naming of polygons is mostly done based on the number of sides as there are some prefix used in terminology which denote a number. For instance, tri means three, thus are flag with three colours is called tricolour, an agreement among three parties is called tripartite agreement, a sports competition with three different activities is called a triathlon, and so on. Similarly, a polygon with three sides or edges and three angles is called a triangle. The other prefixes used are as follows: quadri for 4, penta for 5, hexa for 6, hepta for 7, octa for 8, nona for 9 and deca for 10. Remember, the decagram which equals 10 gm, right? Polygons with sides greater than 10, also have such special names, but we generally denote them with n-gon, where n is the number of sides or edges, as these names are complex and not easy to remember. 

Few polygons have some special names like rectangles, square etc.

Like any other geometrical shapes, polygons also have perimeter, area etc and there are well-devised formulae to find out these properties of a polygon. Let’s know about some of these commonly used formulae. The formulas to find out the areas of some commonly known polygons are as follows: 

Area of a triangle = 1/2 × base × height

Area of a rectangle = length × width

Area of a parallelogram = base × height

Area of a trapezium = 1/2 × (sum of lengths of its parallel sides or bases) × height

Area of a rhombus = 1/2 × product of diagonals

The formula to find out the sum of interior angles of a polygon is 

Sum=(n−2)×180∘ 

Where n = number of sides, for example in case of a pentagon, n is 5.

To find out the value of each interior angle in a regular polygon where all angles are the same, we use the following formula.

Interior Angle=((n-2)×180∘ )/n

To find out the value of each exterior angle in a regular polygon where all angles are the same, we use the following formula.

Exterior Angle=(360∘)/n  as the sum of all angles is always 360◦, and the number of angles is equal to the number of sides.

Whether the polygon is regular or irregular, at each vertex of the polygon sum of an interior angle and exterior angle is 180°. So, when we know one of the angles among the exterior angle and interior angle, we can find out the other angle by putting values in the following formula.

Exterior angle + Interior angle = 180°

To find out the number of diagonals in a polygon, we can use the following formula:

Diagonals=n(n−3)/2

Interestingly, if you look around yourself you can find endless examples of polygons in the real life, all around you. Traffic signboards, slice of pizza faces of pyramids, roof trusses in buildings are examples of triangle. The structure at the Louvre Museum, France is made with joining multiple triangles. Tables are quadrilaterals and can be either square or rectangular. There are many other examples of quadrilaterals in our vicinity. Chessboard, tiles, windows are squares. Book covers, mobile screens, doors are examples of rectangles, a four-sided irregular polygon. Diamond-shaped kites, playing card symbols are examples of rhombus. Leaning ramps, slanted signs are parallelograms, another type of quadrilaterals. Pentagon building (USA) is an architectural example of pentagon, the five-sided polygon. Starfishes, patterns made in rangoli etc are some other examples of pentagons. Honeycomb cells or the cells of a beehive and Snowflakes are shaped like a hexagon. Heptagons are somewhat rare in life but they can be seen in some coins, decorative patterns, and art. Traffic stop signs are octagon, a polygon. Some decorative panels, some mirrors etc are shaped like a octagon. Some dartboards are shaped like a decagon. There are many other examples, where you can see polygonal shapes, if you observe carefully.  To know more about polygons and other mathematical concepts, that too in an interesting way, you can join Bambinos AlphaMaths program where we offer both one on one and group classes. You can join us in this fun and interactive journey of learning maths.

Alpha Math offers a game-based learning experience with a unique four-step approach to mastering every concept in math. Schedule a Free Class Now